Verifying the Semantics of Disambiguation Rules: Using Parse Tree Repairing for Showing Safety and Completeness of Associativity and Priority Rules
Master Project of Luka Miljak

Abstract

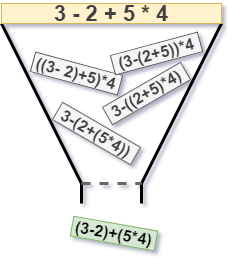
Context-free grammars (CFGs) provide a well-known formalism for the specification of programming languages. They describe the structure of a program in terms of parse trees. One major issue of CFGs is ambiguity, where one sentence can sometimes have multiple different parse trees. Some formalisms like SDF3 or YACC allow annotating a grammar with disambiguation rules, such as priority or associativity. Disambiguation rules filter out certain parse trees, making a grammar less ambiguous. Giving a formal semantics for these disambiguation rules is still an ongoing research topic. In this thesis we verify an existing semantics for these rules by Souza Amorim and Visser (2019) for a subset of expression grammars. These grammars may contain infix, prefix, and postfix expressions. We verify the semantics by proving that it is both safe and complete. Safety states adding disambiguation rules will not change the underlying language of the grammar, meaning each sentence in the language will have at least one valid parse tree that does not get filtered out. Completeness guarantees that a grammar is unambiguous, meaning that each sentence in the language will have at most one valid parse tree that does not get filtered out. We have mechanized the proofs in the Coq Proof Assistant, increasing the confidence in their correctness. As part of the proofs, we also provide a verified implementation for disambiguation rules.

Thesis

• Miljak, Luca. Verifying the Semantics of Disambiguation Rules: Using Parse Tree Repairing for Showing Safety and Completeness of Associativity and Priority Rules. TU Delft Repository, 2021.